Tutta la nostra vita è immersa nell’incertezza: nulla, all’infuori di ciò, si può affermare con certezza.
Bruno De Finetti
Se l’unica nostra certezza è l’incertezza, stando alle parole del matematico statistico Bruno De Finetti, non c’è modo di sottrarsi allo studio dell’incertezza e delle sue sfumature. Anzi, forse è necessario rimettere in discussione tutto ciò che nella quotidianità ha una parvenza di certezza e porre l’attenzione su quegli aspetti di fenomeni apparentemente noti che in realtà non conosciamo.
Fare i conti con un mondo incerto è diventato inevitabile, soprattutto in un’epoca come quella in cui stiamo vivendo in cui conviviamo con eventi e trasformazioni di grande portata e dominati dall’incertezza, come la pandemia o il cambiamento climatico, che mettono alla prova la nostra capacità di confrontarci con l’incerto e gestirlo. Così, il racconto dell’incertezza diventa strumento fondamentale per capire la realtà che ci circonda, e un’occasione per mettere in luce strumenti e competenze che la scienza introduce per comprenderla e governarla.
Da questo proposito nasce la mostra Incertezza. Interpretare il presente, prevedere il futuro a cura di INFN, Vincenzo Barone, Fernando Ferroni, Vincenzo Napolano e Antonella Varaschin, ospitata negli spazi di Palazzo delle Esposizioni a Roma dal 12 ottobre 2021 al 27 febbraio 2022, nell’ambito del più ampio progetto Tre stazioni per Arte-Scienza.
Il lavoro di ricerca e la sperimentazione di tecniche e linguaggi che questa mostra porta con sé fornisce lo spunto per costruire un racconto dell’incertezza, una riflessione su più livelli che passa attraverso l’osservazione di fenomeni, immagini e oggetti in mostra, la fruizione di contenuti multimediali e interattivi, e le parole di studiosi e ricercatori che si confrontano quotidianamente con la nozione di incertezza.
Indice
3. Incertezza, caso, probabilità
Che cos’è l’incertezza
La parola “incertezza” […] è ingannatrice perché sembra riferirsi a una mancanza di certezza o a un’insufficienza di certezza; ma probabilmente la certezza non c’è mai e chi non riesce ad abituarsi a questa idea si condanna a vivere una vita di false certezze.
[E. Boncinelli1, A. Mira2, L’incertezza è una fiera che non si può eliminare ma si può addomesticare, in Incertezza. Interpretare il presente, prevedere il futuro, catalogo della mostra]
“Incertezza” è una parola comune, che pensiamo di poter definire in modo condivisibile; ma una comprensione più profonda del suo significato può essere ricercata nell’etimologia: il termine “certo” deriva dal latino certus e ha la stessa radice di “cernere”, che significa separare, dividere:
Ma cosa si “divide” quando si ritiene di avere delle certezze? Si dice: «Il vero dal falso, ciò che è giusto da ciò che è sbagliato», ma in realtà si dividono, cioè si distinguono, cose simili non interscambiabili. Più acuto è il giudicante, più simili tra di loro sono le cose che sa distinguere. Più è immaginativo e pragmatico, più ci si può fidare di un giudizio di interscambiabilità delle parti. Al contrario, l’incertezza è uno stato mentale e reale in cui non diamo valutazioni di tipo 0 (falso, nero) e 1 (vero, bianco), ma abbiamo a disposizione una graduazione di probabilità, sfumature di grigio, numeri compresi fra 0 ed 1, che assegniamo agli eventi ad indicare il loro livello di verosimiglianza.
[E. Boncinelli1, A. Mira2, L’incertezza è una fiera che non si può eliminare ma si può addomesticare, in Incertezza. Interpretare il presente, prevedere il futuro, catalogo della mostra]
Non solo non esiste una conoscenza certa della realtà – fatto con cui potrebbe essere difficile venire a patti – ma l’incertezza è di fatto ineliminabile; può al massimo essere ridotta e “gestita” affinando le nostre capacità di “cogliere le sfumature”, di misurare ciò che osserviamo e interpretare ciò che misuriamo. Per questo l’incertezza ha un ruolo cruciale per chi si occupa di scienza: risultati quanto più esatti e precisi non possono prescindere da una conoscenza profonda dei limiti delle analisi e degli strumenti scelti. La ricerca scientifica lavora su un doppio binario: costruire strumenti sempre più precisi per la misura e affinare la capacità di isolare i dati dalla loro incertezza, il segnale dal rumore di fondo.
Se ci concentriamo prima sulle attitudini e la pratica della scienza, dobbiamo osservare che, contrariamente alla percezione comune del grande pubblico, gli scienziati non gestiscono la certezza sulla base di ciò che considerano dati infallibili, ma al contrario gestiscono costantemente l’incertezza, sulla base di ipotesi teoriche e di dati, che però mescolano segnale e rumore. Per uno scienziato, la certezza è sempre sostituita da una misura del grado di convinzione e il silenzio non esiste, è semplicemente un “rumore bianco”
[S. Katsanevas3, Suspiciendo Despicio, Despiciendo Suspicio, in Incertezza. Interpretare il presente, prevedere il futuro, catalogo della mostra]
La necessità di individuare le misure più corrette, di isolare i dati rilevanti e distinguerli dalle fluttuazioni legate al caso o allo strumento di misura, ha portato i fisici a fissare rigorosi standard statistici per determinare quando si può dire di aver osservato un nuovo fenomeno con sufficiente certezza – o meglio, incertezza trascurabile. Due risultati recenti sono particolarmente rappresentativi dell’incertezza nella ricerca sperimentale: la misurazione della massa del bosone di Higgs nel 2012 da parte degli esperimenti ATLAS e CMS al CERN di Ginevra, che ha permesso di parlare di scoperta della particella, e quella del momento magnetico anomalo del muone nel 2021, per la quale stando ai dati attuali non è possibile parlare di scoperta, ma è necessario attendere, aumentando i dati raccolti e i controlli su possibili errori legati alla strumentazione. Risultati di così ampia portata devono essere ricercati e verificati scrupolosamente, consapevoli nell’incertezza che portano con sé, imparando a capirla, prevenirla e ridurla:
Esperienze come quelle degli esperimenti ATLAS e CMS mostrano come l’incertezza sia una caratteristica costitutiva della scienza sperimentale, dei suoi metodi e dei suoi processi. […] È necessaria, dunque, una notevole cautela prima di annunciare una scoperta scientifica, nonostante la tentazione molto umana di cedere all’entusiasmo. E non bisogna dimenticare che, sebbene la fisica sia popolarmente nota per le sue grandi scoperte, essa progredisce grazie a un lavoro lungo, costante e accurato di addomesticamento dell’incertezza.
[A. Zoccoli4, La logica della scoperta, in Incertezza. Interpretare il presente, prevedere il futuro, catalogo della mostra]
Incertezza e misura
Misurare genera informazione e l’informazione è fondamentale per creare conoscenza. L’informazione può essere intesa come la soluzione parziale al problema dell’incertezza, poiché consente di rispondere a domande relative all’essenza di un’entità e alla natura delle sue caratteristiche. Pertanto, misurare è essenziale nel processo scientifico di formulazione e verifica di un’ipotesi. D’altra parte, l’incertezza è legata a situazioni in cui l’informazione è imperfetta o assente.
[D. Wiersma5, L’importanza di fare misure sempre più precise, in Incertezza. Interpretare il presente, prevedere il futuro, catalogo della mostra]
Le nostre osservazioni sul mondo sono sempre accompagnate da un inevitabile margine di incertezza. Un’incertezza che dipende dagli strumenti che utilizziamo, da fluttuazioni casuali, dall’aleatorietà delle condizioni di misura, e che è intrinseca al processo di misura e perciò ineliminabile. Fernando Ferroni6, uno dei curatori della mostra Incertezza, lo spiega così:
Ascolta “Misure ed errori – Fernando Ferroni” su Spreaker.
Per leggere la trascrizione della clip, clicca sul tasto i.
Anche quando il processo di misura è automatizzato e si riduce così l’errore che come esseri umani possiamo compiere nel misurare, l’incertezza è comunque presente. Ne è una dimostrazione, nella mostra Incertezza,un’installazione in cui un braccio meccanico automatizzato solleva ripetutamente un peso di metallo da un kilogrammo e lo depone su una bilancia, registrando di volta in volta il risultato. Nonostante le misure vengano ripetute dal braccio in modo identico e senza cambiare il peso né la bilancia, la massa misurata è sempre leggermente diversa.

Il processo di misura del pesetto viene ripetuto sempre allo stesso modo, ma il risultato varia leggermente di volta in volta.
La ricerca della precisione nel processo di misura diventa ancor più importante quando si tratta di stabilire le unità di misura, sulla base delle quali quantifichiamo le grandezze fisiche. Il sistema di misura più diffuso, che adottiamo anche noi, è il Sistema internazionale delle unità di misura (SI). Fino a qualche anno fa, il SI si basava su sette unità di misura fondamentali: il kilogrammo per la massa, il metro per le distanze, il secondo per il tempo, il kelvin per la temperatura, l’ampere per l’intensità di corrente elettrica, la mole per la quantità di sostanza, la candela per l’intensità luminosa. In Italia, a garantire la realizzazione, il mantenimento e lo sviluppo delle unità di misura del SI è l’Istituto Nazionale di Ricerca Metrologica (INRiM). Dal 2019, tutte le unità di misura fondamentali non sono più definite per mezzo di campioni fisici, che potrebbero subire delle alterazioni nel tempo, ma facendo riferimento a delle costanti fisiche. Alle sette unità fondamentali sono state quindi associate sette costanti, che, in quanto costanti della fisica, non possono dipendere dal campione di riferimento, ma sono state misurate nel modo più accurato possibile. L’ultima unità di misura a essere ridefinita è stata il kilogrammo: dal 1889, la sua definizione coincideva con la massa di un cilindro di platino-iridio che costituiva il prototipo internazionale del chilogrammo, che poteva però variare leggermente nel tempo per il deposito di contaminanti; dal 2019, il kilogrammo è definito invece sulla base della costante di Planck.
Misure sempre più precise e affidabili sono fondamentali per l’industria, l’ambiente, la salute, ma sono anche la chiave per addentrarsi di più nei misteri dell’universo:
Gli scienziati amano l’incertezza. La adorano! Esplorando il territorio dell’incertezza, uno scienziato è in grado di scoprire nuovi fenomeni, verificare o confutare modelli e scovare sempre nuovi dettagli per spiegare il mondo.
[D. Wiersma5, L’importanza di fare misure sempre più precise, in Incertezza. Interpretare il presente, prevedere il futuro, catalogo della mostra]
Nonostante sia ineliminabile, l’incertezza sperimentale può però essere ridotta, e la ricerca scientifica si muove anche in questa direzione: apparati di misura sempre più precisi possono essere determinanti per compiere nuove scoperte. Un esempio fra tutti sono le onde gravitazionali, misurate per la prima volta nel 2015, cento anni dopo la loro previsione da parte di Albert Einstein nella sua teoria della relatività generale.
Per rivelare queste oscillazioni quasi impercettibili dello spaziotempo, è stato necessario costruire particolari strumenti di misura, in grado di misurare spostamenti piccolissimi: gli interferometri per onde gravitazionali. Le osservazioni del 2015 si devono ai due interferometri dell’esperimento LIGO, installati in USA rispettivamente in Louisiana e nello stato di Washington, e alla collaborazione internazionale cui l’Italia partecipa con l’esperimento Virgo, installato a Cascina, in provincia di Pisa.
Il video mostra il funzionamento di un interferometro per onde gravitazionali. L’interferometro è costituito da due bracci perpendicolari lunghi qualche chilometro, all’interno dei quali viaggiano fasci laser; giunti alle estremità, i due fasci vengono riflessi da due specchi e si ricongiungono, formando un’immagine particolare, chiamata figura di interferenza. Una variazione della lunghezza dei bracci, anche se piccolissima come quella generata dalle onde gravitazionali – che al loro passaggio, deformando lo spaziotempo, ne allungano uno mentre accorcialo l’altro–, causa una variazione della distanza degli specchi e quindi della lunghezza del percorso del laser. Di conseguenza, si modifica anche la figura di interferenza.
Anche strumenti estremamente precisi, tuttavia, non possono aggirare completamente l’incertezza. Per comprendere ciò che misuriamo dobbiamo affinare la capacità di analizzare i dati raccolti nel processo di misura per interpretarli correttamente, riconoscendo e tenendo in conto le sorgenti di errore che non possiamo rimuovere e facendo appello anche a uno degli strumenti matematici più potenti per “imbrigliare” il caso: la teoria della probabilità.
Incertezza, caso, probabilità
Che cos’è la probabilità, come definirla? Può sembrare un’impresa da niente, ma provateci voi a farlo: non è affatto facile; tutti pensiamo di sapere che cosa sia la probabilità, ma non siamo in grado di definirla.
[G. Parisi7, Il valore dell’incertezza, in Incertezza. Interpretare il presente, prevedere il futuro, catalogo della mostra]
La teoria della probabilità è oggi uno degli strumenti matematici di cui le scienze naturali, e anche le scienze sociali, si servono per descrivere la realtà e valutarne l’incertezza. Tuttavia, alle sue origini c’è la risoluzione di problemi molto distanti, che riguardano i giochi di fortuna. Alcune menti brillanti come Blaise Pascal e Pierre de Fermat si occuparono già nel Seicento di questioni di questo tipo, ma i primi elementi di teoria della probabilità si devono a Girolamo Cardano che, a metà del Cinquecento, dedicò uno scritto al gioco dei dadi, argomento su cui si sarebbe soffermato più avanti anche Galileo Galilei.
La teoria prende una forma più definita nel secolo successivo, grazie agli studi di Jackob Bernoulli e Pierre-Simone de Laplace, dedicati alla cosiddetta “legge dei grandi numeri”; a metà del Settecento viene anche formulato il teorema di Bayes sulla probabilità condizionata, ovvero la probabilità di un evento condizionata da un altro evento, ancora oggi di fondamentale importanza per l’analisi dell’esito di un esame clinico, per esempio.
La vera rivoluzione arriva però nel Novecento, con Bruno de Finetti, che introduce una nuova idea di probabilità come misura della nostra “ragionevole” aspettativa del verificarsi di un evento. Con questa nuova definizione, il calcolo delle probabilità si conferma sempre di più come una guida coerente ed efficace per ragionare e agire in condizioni di incertezza.
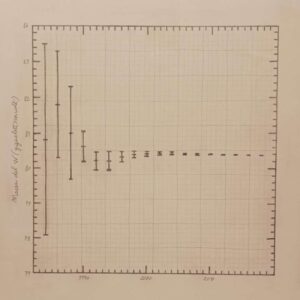
Per alcune grandezze, come per la massa del bosone W, le barre d’errore si sono progressivamente ridotte nel tempo grazie allo sviluppo di strumenti e procedure di misura sempre più precise.
Un modo molto chiaro di visualizzare l’incertezza di una misura e il suo legame con la probabilità sono le barre di errore che si possono tracciare attorno al valore misurato. A causa di errori casuali o sistematici o di limiti veri e propri, infatti, ciascun valore frutto di una misura, diretta o indiretta, non corrisponde esattamente al valore “vero” della grandezza misurata. Per questo, il valore misurato è sempre associato a un intervallo di valori entro il quale ci si aspetta, con una certa probabilità, che sia collocato il valore “vero” della grandezza. Questo intervallo graficamente è rappresentato dalle barre d’errore.
Per ridurre l’incertezza si cerca di minimizzare gli errori durante le misure e di migliorare sempre di più gli strumenti e le tecniche di misura. In questi grafici viene mostrata l’evoluzione nel tempo delle barre d’errore attorno al valore di alcune grandezze: più sono piccole le barre più ci si avvicina alla conoscenza del valore “vero”.

Dopo aver pronunciato al microfono una sequenza di 0 e 1, un algoritmo calcolerà l’entropia di Shannon, parametro che stima l’imprevedibilità, la casualità di una sequenza di valori.
Parallelamente al progredire della precisione degli strumenti e dell’accuratezza nelle misure, la matematica dell’ultimo secolo ha sviluppato e affinato le capacità di interpretare l’incertezza, ma non solo: oggi siamo in grado di descrivere e quantificare l’imprevedibilità di un processo. La possibilità di stimare la casualità è cruciale per processi che si basano su sequenze di valori casuali, come la crittografia dei dati. Un parametro utile in tal senso è l’entropia di Shannon, introdotta nel 1984 dal matematico Claude Shannon, che assume un valore tanto più grande quanto più la sequenza di simboli è casuale. Poiché il nostro cervello tende a ricreare involontariamente sequenze che contengono elementi di ordine e regolarità, nonostante i nostri sforzi non riusciamo a generare una sequenza totalmente casuale; simulare una perfetta casualità è impossibile anche per i più potenti computer. Un’installazione realizzata per la mostra “Incertezza” permette di stimare quanto possiamo avvicinarci alla totale casualità, calcolando il valore dell’entropia di Shannon per una sequenza di 0 e 1 pronunciati a un microfono.
Ascolta “Zero e uno – Fernando Ferroni” su Spreaker.
Per leggere la trascrizione della clip, clicca sul tasto i.
Nonostante la teoria della probabilità sia una risorsa chiave per interpretare e conoscere il mondo attraverso la comprensione dell’incertezza, i progressi conoscitivi dell’ultimo secolo ci hanno posto davanti al fatto che, per alcuni fenomeni in particolare, l’incertezza è un elemento ineliminabile. Il mondo quantistico e i fenomeni caotici ci costringono a relazionarci con una forma di incertezza che non dipende più dai nostri strumenti o dal numero di misure che riusciamo a compiere, ma è un dato intrinseco nella struttura della realtà.
1Edoardo Boncinelli, Fisico e genetista, Università Vita-Salute San Raffaele
2Antonietta Mira, Statistica, Università della Svizzera Italiana
3Stavros Katsanevas, Fisico, EGO European Gravitational Observatory, Université Paris Diderot
4Antonio Zoccoli, Fisico, INFN Istituto Nazionale di Fisica Nucleare, Universit. degli Studi di Bologna
5Diederik Wiersma, Fisico, INRiM Istituto Nazionale di Ricerca Metrologica, LENS European Laboratory for Non-linear Spectroscopy, Università di Firenze
6 Fernando Ferroni, Fisico, GSSI Gran Sasso Science Institute, INFN Istituto Nazionale di Fisica Nucleare, Azienda Speciale Palaexpo






